6174 - Kaprekar's Constant: Test in Python.

6174 - doesn't seem like a very interesting number at first glance but this Numberphile video shows that all four digit numbers converge to this number if the following procedure is followed:

1. Start with a four digit number. (All four digits cannot be the same).
2. Sort the digits in descending order -> D
3. Sort the digits in ascending order -> A
4. Take the difference between D and A.
5. Repeat steps 1-4 with the new number -> D-A.

The answer will always converge to 6174!

I wrote a little function in python to test this out:

def difference(numbers: list, verbose=True):
    if verbose: print(f"Calling function with {numbers}")
    # numbers = [int(i) for i in str(number)]

    desc = int(''.join([str(i) for i in sorted(numbers, reverse=True)]))
    asc = int(''.join([str(i) for i in sorted(numbers)]))

    diff = desc - asc
    if verbose: print(f'{desc}-{asc} = {diff}\n')

    if diff == 0:
        if verbose: 
        	print("Did not converge! All digits in the number are the same!")
        return False

    elif diff == 6174:
        if verbose: print("Converged!")
        return 1

    else:
        count = difference([int(i) for i in str(diff)], verbose)
        if count:
            count += 1
        else:
            count = False

        return count

Example

Let's look at an example using the numbers 3 2 4 5.

difference([3,2,4,5])

Output:

Calling function with [3, 2, 4, 5]
5432-2345 = 3087
Calling function with [3, 0, 8, 7]
8730-378 = 8352
Calling function with [8, 3, 5, 2]
8532-2358 = 6174
Calling function with [6, 1, 7, 4]
7641-1467 = 6174

Converged!

3

In this case it took 3 iterations to converge to 6174.

Test for all four digit numbers.

I had to check for myself if this claim held for all four digit numbers, so I used the itertools module to test it:

from itertools import product

non_converging = []
counts = []

n_attempts = 0
n_success = 0
numbs_attempted = []

for numbers in list(product(range(10), repeat=4)):

    # All numbers cannot be the same, differnece is 0!
    if len(set(numbers)) > 1:
        n_attempts += 1
        try:
            count = difference(list(numbers), verbose=False)
            if count:
                counts.append(count)
                n_success += 1
                numbs_attempted.append(numbers)
            else:
            	non_converging.append(numbers)
        except RecursionError:
        	non_converging.append(numbers)

print(f"Total numbers attempted: {n_attempts}")
print(f"Successfully converged = {n_success}")

print(f"Non converging: {len(non_converging)}")
print(non_converging)

print(f"Maximum iterations to converge: {max(counts)}")

Output:

Total numbers attempted: 9990
Successfully converged = 9918
Non converging: 72
[(0, 0, 0, 1), (0, 0, 1, 0), (0, 1, 0, 0), (0, 1, 1, 1), (1, 0, 0, 0), (1, 0, 1, 1), (1, 1, 0, 1), (1, 1, 1, 0), (1, 1, 1, 2), (1, 1, 2, 1), (1, 2, 1, 1), (1, 2, 2, 2), (2, 1, 1, 1), (2, 1, 2, 2), (2, 2, 1, 2), (2, 2, 2, 1), (2, 2, 2, 3), (2, 2, 3, 2), (2, 3, 2, 2), (2, 3, 3, 3), (3, 2, 2, 2), (3, 2, 3, 3), (3, 3, 2, 3), (3, 3, 3, 2), (3, 3, 3, 4), (3, 3, 4, 3), (3, 4, 3, 3), (3, 4, 4, 4), (4, 3, 3, 3), (4, 3, 4, 4), (4, 4, 3, 4), (4, 4, 4, 3), (4, 4, 4, 5), (4, 4, 5, 4), (4, 5, 4, 4), (4, 5, 5, 5), (5, 4, 4, 4), (5, 4, 5, 5), (5, 5, 4, 5), (5, 5, 5, 4), (5, 5, 5, 6), (5, 5, 6, 5), (5, 6, 5, 5), (5, 6, 6, 6), (6, 5, 5, 5), (6, 5, 6, 6), (6, 6, 5, 6), (6, 6, 6, 5), (6, 6, 6, 7), (6, 6, 7, 6), (6, 7, 6, 6), (6, 7, 7, 7), (7, 6, 6, 6), (7, 6, 7, 7), (7, 7, 6, 7), (7, 7, 7, 6), (7, 7, 7, 8), (7, 7, 8, 7), (7, 8, 7, 7), (7, 8, 8, 8), (8, 7, 7, 7), (8, 7, 8, 8), (8, 8, 7, 8), (8, 8, 8, 7), (8, 8, 8, 9), (8, 8, 9, 8), (8, 9, 8, 8), (8, 9, 9, 9), (9, 8, 8, 8), (9, 8, 9, 9), (9, 9, 8, 9), (9, 9, 9, 8)]
Maximum iterations to converge: 7

It works for except for 9918 out of 9990 combinations of four digits where all digits are not the same. The instances where it doesn't converge to 6174 are when 3 of the digits are the same number and the remaining digit is +/- 1 of the same number. In this cases the result from the first iteration is 999, the next one results in 0 and  then the procedure cannot continue anymore.

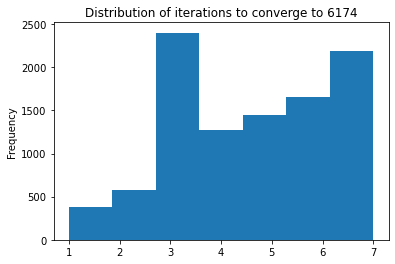
The plot below shows the distribution of the number of iterations it takes to converge to 6174. The mode is 3 iterations and the mean 4.67.

Full code can be found on GitHub .